最早向我们展示圆的面积与半径的平方成正比关系的荣誉是Cnidus的Eudoxus(约公元前400-350年)。在今天的代数符号,即比例由熟悉公式A =πR表示2。然而,尽管比例常数π很熟悉,但它仍然是高度神秘的,寻求理解并找到其精确值的探索已经在数学家中占据了数千年的历史。欧多克斯后一个世纪,阿基米德发现π的第一良好的近似:3 10 / 71 <π<3 1 / 7。他通过用一个96边的多边形近似一个圆来实现此目的(请参见动画)。通过使用具有更多边的多边形,可以找到更好的近似值,但是它们只能加深奥秘,因为无法获得确切的值,并且在近似序列中也看不到任何模式。
谜的一个惊人的溶液被发现由约1500 CE印度数学家:π可由无限表示,但令人惊讶的简单,系列π / 4 = 1 - 1 / 3 + 1 / 5 - 1 / 7 +⋯。他们发现这作为该系列的反正切函数的一种特殊情况:黄褐色-1(X)= X - X 3 / 3 + X 5 / 5 - X 7 / 7 +⋯。
这些结果的个别发现者并不确定。有些学者将其归功于Nilakantha Somayaji,有些归功于Madhava。印度的证据在结构上与后来詹姆斯·格里高利,戈特弗里德·威廉·莱布尼兹和雅各布·伯努利在欧洲发现的证据相似。主要区别在于,在欧洲人利用微积分基本定理的优势的情况下,印度人不得不寻找形式和的极限
在格雷戈里(Gregory)重新发现约1670年的反正切序列之前,在欧洲发现了π的其他公式。1655年,约翰·沃利斯(John Wallis)发现了无限乘积π / 4 = 2 / 3 ∙ 4 / 3 ∙ 4 / 5 ∙ 6 / 5 ∙ 6 / 7 ⋯,他的同事William Brouncker将其转换为无限连续分数
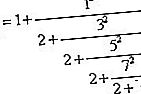
最后,在欧拉的简介无限的分析(1748),系列π / 4 = 1 - 1 / 3 + 1 / 5 - 1 / 7 +⋯被变换成Brouncker的持续部分,这表明所有的三个公式是在有些感觉是一样的。
Brouncker的无限连续分数特别重要,因为它表明π不是普通分数-换句话说,π是不合理的。约翰·兰伯特(Johann Lambert)在1767年给出的第一个证明π是非理性的精确地证明了这一思想。













