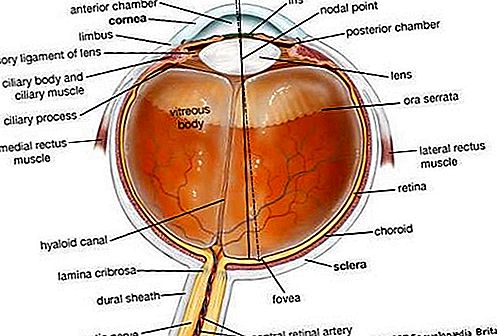
图论的应用
平面图
如果曲线图G可以以这样的方式表示在平面上,即顶点都是不同的点,边线是简单曲线,并且没有两个边线在它们的末端相遇,则称该图形为平面。例如,如图4A所示,四个顶点上的完整图K 4是平面的。

如果可以通过边的细分从同一张图中获得两个图,则这两个图被称为同胚。例如,图4A和图4B中的图是同胚的。
K m,n图是可将其顶点集划分为两个子集的图,一个子集包含m个顶点,另一个子集包含n个顶点。同一子集的任意两个顶点不相邻,而不同子集的任意两个顶点相邻。波兰数学家Kazimierz Kuratowski在1930年证明了以下著名定理:
图G是平面的必要和充分条件是它不包含图5中所示的K 5或K 3,3同胚的子图。

图G的基本收缩是G到新图G 1的变换,这样G的两个相邻顶点u和υ被G 1中的新顶点w替换,而w在G 1中与所有顶点G相邻。u或υ在G中相邻。如果可以通过一系列基本收缩从G获得G *,则图G *被认为是G的收缩。以下是德国数学家K.Wagner在1937年提出的平面图的另一个特征。
一个图形是平面的,当且仅当它对于K 5或K 3,3不可收缩。
四色图问题
一个多世纪以来,四色图问题的解决方案一直困扰着每位尝试过此方法的分析师。这个问题也许引起了莫比乌斯的注意,但是第一次书面提及似乎是一位弗朗西斯·格斯里(Francis Guthrie)于1852年给他的弟弟奥古斯都·德摩根的学生的信。
问题与平面贴图有关,也就是说,将平面细分成由简单闭合曲线界定的非重叠区域。在地理地图中,根据经验,在尝试过的许多特殊情况下,最多需要四种颜色才能对区域着色,以便共享公共边界的两个区域始终具有不同的颜色,在某些情况下,至少需要四种颜色。(仅在某个点会合的区域(例如美国的科罗拉多州和亚利桑那州)不被视为具有共同边界)。这种经验观察的形式化构成了所谓的“四色定理”。问题是要证明或否定每个平面图都是这种情况的断言。容易证明三种颜色不足,而英国数学家PJ Heawood于1890年证明了五种颜色的充分性。
1879年,英国人AB Kempe提出了四色问题的解决方案。尽管海伍德(Heawood)表明肯普(Kempe)的论点是有缺陷的,但其两个概念在后来的调查中证明是卓有成效的。其中一种被称为不可避免性,它正确地说明了构建不存在四种配置中的每一种的地图的可能性(这些配置包含一个具有两个邻居,一个具有三个邻居,一个具有四个邻居和一个具有五个邻居的区域)。第二个概念,即约简性,取自Kempe的有效证明,即如果有一张地图需要至少五种颜色并且包含一个具有四个(或三个或两个)邻居的区域,那么必须有一个地图需要五个少数区域的颜色。肯普(Kempe)试图证明包含五个邻域的地图的可简化性的尝试是错误的,但是在1976年美国肯尼思·阿佩尔(Kenneth Appel)和沃尔夫冈·哈肯(Wolfgang Haken)发表的证明中对此进行了纠正。他们的证据引起了一些批评,因为它需要评估1,936个不同的案例,每个案例涉及多达500,000个逻辑运算。Appel,Haken及其合作者设计了程序,使大型数字计算机可以处理这些细节。该计算机需要1000多个小时来执行任务,并且所得到的正式证明长达数百页。
欧拉循环与柯尼斯堡桥问题
多重图形G由顶点的非空集合V(G)和V(G)的不同元素的无序对的集合的子集E(G)组成,频率f≥1附加到每对上。如果频率为f 的对(x 1,x 2)属于E(G),则顶点x 1和x 2通过f边连接。
多重图形G的欧拉循环是一条闭合链,其中每个边恰好出现一次。欧拉证明,当且仅当多图连接(除孤立点之外)且奇数顶点的数量为零或两个时,它才具有欧拉循环。
首先以以下方式出现此问题。由两个分支汇合而成的普雷格尔河穿过柯尼斯堡(Königsberg)镇,流向克尼普霍夫(Kneiphof)岛的两侧。如图7A所示,有七个桥。市民们想知道是否有可能去散步并一次又一次地跨过每座桥梁。这等效于为图6B中的多重图找到欧拉循环。欧拉证明这是不可能的,因为有四个奇数个顶点。