微分方程

微分方程包含一个或多个导数的数学陈述，即代表连续变化量变化率的术语。微分方程在科学和工程学以及定量研究的许多其他领域中非常普遍，因为可以直接观察和测量发生变化的系统的变化率。通常，微分方程的解是表示一个变量对一个或多个变量的功能依赖性的方程。它通常包含原始微分方程中不存在的常数项。换句话说，微分方程的解产生了一个函数，该函数至少在某些约束条件下可以用来预测原始系统的行为。

分析：牛顿和微分方程

。

分析的应用是微分方程，将各种数量的变化率与其当前值相关联，

。

微分方程分为几大类，而这些又又分为许多子类。最重要的类别是常微分方程和偏微分方程。当方程中涉及的函数仅取决于单个变量时，其导数为常导数，并且将微分方程归类为常微分方程。另一方面，如果函数依赖于几个独立变量，则其导数为偏导数，则将微分方程分类为偏微分方程。以下是常微分方程的示例：

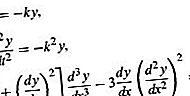
在这些函数中，y代表函数，t或x是自变量。符号k和m在这里用来表示特定的常数。

不管是哪种类型，如果微分方程包含n阶导数，但不包含高于此阶数的导数，则称该微分方程为n阶。该方程式是二阶偏微分方程式的示例。常微分方程和偏微分方程的理论明显不同，因此将这两类分开对待。

代替单个微分方程，研究的对象可以是此类方程的同时系统。动力学定律的制定经常导致这种系统。在许多情况下，n阶单个微分方程可以用n个联立方程组替换，每个方程组都是一阶的，因此可以应用线性代数的技术。

一个普通的微分方程，其中函数和自变量由y表示，而x实际上是y的基本特征随x的隐式概括。如果可以生成y的明确公式，则可能更容易分析这些特征。从微分方程式可推导的这样的公式或至少x和y中的方程式（不涉及导数）被称为微分方程式的解。通过代数和微积分的应用从方程式推导解的过程称为求解或积分方程式。但是，应该指出的是，可以明确求解的微分方程只有少数。因此，大多数功能必须通过间接方法进行研究。如果不可能生产它，甚至必须证明它的存在。在实践中，采用涉及计算机的数值分析方法来获得有用的近似解。