Riemann假设,在数论中,是德国数学家Bernhard Riemann提出的关于Riemann zeta函数解位置的假设,该假设与素数定理有关,对素数的分布具有重要意义。里曼将该假设包括在1859年11月版的《柏林国民报》(Monatsberichte der Berliner Akademie)上发表的论文《论数量少于给定数量的素数上》中。柏林学院”)。
zeta函数定义为无限级数ζ(s)= 1 + 2 -s + 3 -s + 4 -s +⋯,或者用更紧凑的表示形式,
,其中n的项之和(Σ)通过正整数从1到无穷大,而s是大于1的固定正整数。zeta函数最早是由瑞士数学家Leonhard Euler在18世纪研究的。(由于这个原因,有时将其称为Euler zeta函数。对于ζ(1),该序列只是谐波序列,自上古以来就无限增加,即众所周知,即其总和是无限的。)Euler当他证明1735该ζ(2)=π 2 /6,即已经躲避时代的最伟大的数学家,包括瑞士伯努利家族(雅各布,约翰,和丹尼尔)的问题。更一般地说,欧拉(1739)发现偶数整数的zeta函数值与伯努利数之间的关系,伯努利数是x /(e x − 1)的泰勒级数展开中的系数。(另请参见指数函数。)更令人惊奇的是,1737年,欧拉发现了一个与zeta函数有关的公式,该公式涉及将包含正整数的无限项序列求和,并且涉及每个素数的无限乘积:
Riemann扩展了zeta函数的研究,以包括复数x + iy,其中i =√-1的平方根,除了复平面中的x = 1线。黎曼(Riemann)知道,对于所有负偶数-2,-4,-6,
。
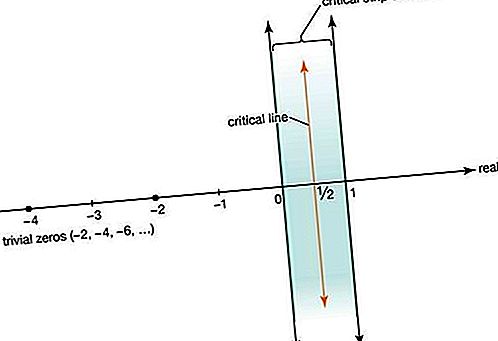
(所谓的平凡零),并且它在严格落在x = 0和x = 1线之间的复数临界带中具有无限个零。他还知道,所有非平凡零点都相对于临界直线x = 1 / 2。黎曼猜想所有非平凡零点都在临界线上,这一猜想后来被称为黎曼假设。
在1914年英国数学家戈弗雷哈罗德哈代证明,ζ的溶液(S)的无限数量=上临界线x = 0时存在的1 / 2。随后,各种数学家证明,大部分解决方案必须位于临界线上,尽管所有非平凡解决方案都经常出现的“证明”存在缺陷。计算机也已用于测试解决方案,其中前10万亿个非平凡的解决方案显示在关键线上。
黎曼假设的证明对于数论和密码学中质数的使用将产生深远的影响。
黎曼假设长期以来一直被认为是数学中最大的未解决问题。它是1900年8月8日在巴黎举行的第二届国际数学大会上,德国数学家戴维·希尔伯特(David Hilbert)提出的20世纪数学家所面临的10个未解决的数学问题之一(印刷地址中的23个)。2000年,美国数学家斯蒂芬(Stephen)斯玛德(Smale)列举了21世纪的重要问题,从而更新了希尔伯特(Hilbert)的想法;黎曼假设是第一位的。在2000年,它被指定为“千年问题”,这是美国马萨诸塞州剑桥的克莱数学研究所选择的七个数学问题之一,并获得了特别奖。每个“千年问题”的解决方案价值100万美元。在2008年,美国国防部高级研究计划局(DARPA)将其列为DARPA数学挑战之一,它正在征求其资助研究建议的23个数学问题—“数学挑战十九:解决黎曼假说”。数论的圣杯。”