月亮的正交

希俄斯的希波克拉底（约公元前460年）证明，圆弧之间的月亮形区域（称为月球）可以精确地表示为直线区域或正交区域。在下面的简单情况下，围绕直角三角形的侧面形成的两个月球的合并面积等于该三角形的合并面积。

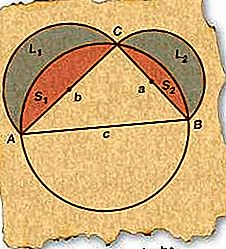
从右边的ΔABC开始，画一个圆，其直径与斜边AB（c面）重合。因为任何直角三角形的斜边都必须用圆的直径来绘制，所以C必须在圆上。
如图所示，绘制直径为AC（b面）和BC（a面）的半圆。
如图所示，标记最终的月牙L ₁和L ₂以及最终的段S ₁和S ₂。
现在，凸角（L ₁和L ₂）的总和必须等于包含半圆的半圆（L ₁ + S ₁和L ₂ + S ₂）的总和减去两个线段（S ₁和S ₂）。因此，L ₁ + L ₂ = ^π / ₂（^b / ₂）² -S ₁ + ^π / ₂（^a / ₂）² -S ₂（因为圆的面积是半径的平方的π倍）。
段的总和（S ₁和S ₂）等于基于AB的半圆的面积减去三角形的面积。因此，S ₁ + S ₂＝^π / ₂（^c / ₂）² -ΔABC。
将第5步中的表达式代入第4步中，并排除常用项L ₁ + L ₂ = ^π / ₈（a ² + b ² -c ²）+ΔABC。
由于∠ACB= 90°，根据勾股定理，a ² + b ² -c ² = 0。因此，L ₁ + L ₂＝ΔABC。

希波克拉底设法使几种月牙都成正方形，有些月牙弧的半径大于或小于半圆，尽管他可能还没有相信，但他暗示他的方法可以使整个圆角平方。在古典时代的末期，Boethius（约公元470-524年）用欧几里得的摘要翻译成拉丁语，使几何图形的光闪烁了半个世纪，他提到有人完成了圆的平方。未知的天才是否使用过月球或其他方法是未知的，因为Boethius由于缺乏空间而没有进行演示。因此，他传达了圆的正交性的挑战以及显然对执行圆环有用的几何碎片。欧洲人在启蒙运动中一直肩负着不幸的任务。最终，在1775年，巴黎科学院厌倦了在提交给它的许多解决方案中发现谬论的任务，拒绝与圆形平方器有任何进一步的关系。