张量分析数学

张量分析，与关系或法则有关的数学分支，无论用于指定数量的坐标系如何，都有效。这种关系称为协变。发明了张量作为向量的扩展，以形式化数学流形研究中出现的几何实体的操纵。

向量是具有大小和方向的实体。它可以通过箭头绘制来表示，并根据平行四边形定律与相似的实体结合。由于该定律，向量具有分量-每个坐标系的集合不同。当坐标系改变时，矢量的分量根据可从平行四边形定律推导出的变换的数学定律改变。组件的转换定律具有两个重要特性。首先，在原始坐标系中结束了一系列更改之后，向量的成分将与开始时相同。其次，向量之间的关系（例如，三个向量U，V，W，使得2U + 5V = 4W）将存在于组件中，而与坐标系无关。

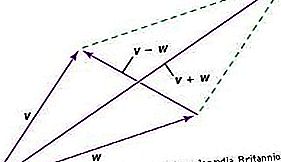
因此，矢量可以被视为在n维空间中具有n个分量的实体，该n个分量根据具有上述特性的特定变换定律进行变换。向量本身是一个独立于坐标的目标实体，但是对于所有坐标系均处于平等位置的组件，将其进行处理。

在不坚持图片图像的情况下，张量定义为具有根据矢量向量定律的概括但仍保留该定律的两个关键特性的变换定律变化的分量的客观实体。为了方便起见，坐标通常从1到n进行编号，并且张量的每个分量由带有上标和下标的字母表示，每个上标和下标分别取值为1到n。因此，由分量T ^ab _c表示的张量将具有n ^3个分量，因为a，b和c的值从1到n。标量和向量构成张量的特殊情况，前者每个坐标系仅具有一个分量，而后者具有n。张量分量之间的任何线性关系，例如7R ^a _bcd + 2S ^a _bcd -3T ^a _bcd = 0，如果在一个坐标系中有效，则对所有坐标都是有效的，因此尽管存在这样的关系，但它表示的是客观且独立于坐标系的关系缺乏图片代表。

两个张量，称为度量张量和曲率张量，特别令人关注。度量张量用于例如将向量分量转换为向量的大小。为简单起见，请考虑具有简单垂直坐标的二维情况。令向量V具有分量V ₁，V ₂。然后，根据应用于直角三角形OAP的勾股定理，V的平方由OP ² =（V ₁）² +（V ₂）^2给出。

该方程式中隐藏的是度量张量。它是隐藏的，因为此处包含未写入的0和1。如果方程式以以下形式重写：OP ² = 1（V ₁）² + 0V ₁ V ₂ + 0V ₂ V ₁ +1（V ₂）²，度量张量的全套分量（1、0、0、1）显而易见。如果使用倾斜的坐标，为OP式²采用的更一般formOP ² = G ₁₁（V ₁）² + G ₁₂ V ₁ V ₂ + G ₂₁ V ₂ V ₁ +克₂₂（V ₂）²，数量g ₁₁，g ₁₂，g ₂₁，g ₂₂是度量张量的新成分。

从度量张量中，可以构造一个复杂的张量，称为曲率张量，它表示它所属于的n维空间的固有曲率的各个方面。

张量在几何和物理中有许多应用。在建立广义相对论时，爱因斯坦（Albert Einstein）指出，无论使用什么坐标系，物理定律都必须相同。这导致他用张量方程表达这些定律。从他的相对论这一特殊理论中已经知道，时间和空间是如此紧密地联系在一起，以致构成了不可分割的四维时空。爱因斯坦推测，万有引力只能用四维时空的度量张量来表示。为了表达相对论的引力定律，他以公制张量和由其形成的曲率张量作为构建块。一旦他决定将自己限制在这些构造块上，它们的匮乏就使他产生了一个关于引力定律的本质上唯一的张量方程，其中引力不是作为力出现的，而是时空曲率的体现。

尽管对张量进行了较早的研究，但正是爱因斯坦的相对论的成功引起了数学家和物理学家对张量及其应用的当前广泛兴趣。